Globally optimal registration methods
Linearized forms of non-minimal geometric problems are able to retrieve a unique and thus globally optimal solution. However they often do so under a simplified algebraic, least sum-of-squares error criterion (e.g. EPnP), or by ignoring side-constraints on the solution variable (e.g. 8-point algorithm for essential matrix estimation applied over n points). The original, non-simplified objective often appears in the form of a non-linear optimization problem, which in principle requires the use of iterative non-linear optimization techniques. Iterative non-linear optimization, however, does no longer guarantee the identification of a globally optimal solution. The following represents a series of problems which–despite their complexity and non-linearity–have still been solved globally optimally by employing branch-and-bound optimization, convex optimization, or polynomial optimization.
Globally optimal, correspondences-free camera registration
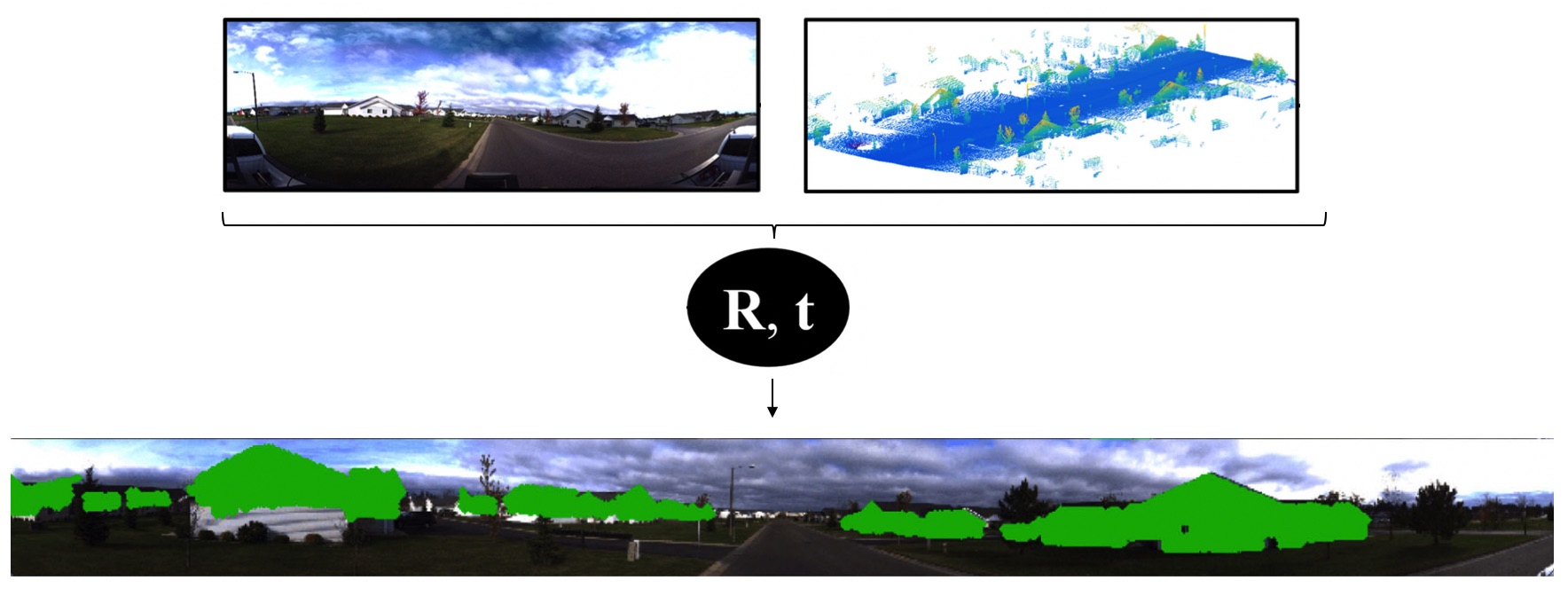
Together with former collaborators at ANU, Prof. Kneip has worked on a novel method for estimating the 6-DoF pose of a camera from a single image relative to a pre-computed 3D point-set, and notably in the situation where no 2D-3D point correspondences can be established owing to the lack of descriptors. Prior approaches to the simultaneous pose and correspondence problem use local optimisation, and are therefore unlikely to find the optimal solution without a good pose initialisation. Other prior art introduces restrictive prior assumptions. Since a large proportion of outliers are common for this problem, the present method instead proposes a globally-optimal inlier set cardinality maximisation approach which jointly estimates optimal camera pose and optimal correspondences. The approach employs branch-and-bound to search the 6D space of camera poses, guaranteeing global optimality without requiring a pose prior. The method has been awarded by the Marr Prize (honourable mention), one of the most prestiguous best paper awards in the computer vision community. Follow-up research investigates a similar globally optimal alignment of Spherical Mixture Models, or an application to globally optimal pose and correspondence for the image to image registration problem of a downward-facing camera mounted on an Ackermann vehicle.
D Campbell, L Petersson, L Kneip, and H Li. Globally-Optimal Inlier Set Maximisation for Simultaneous Camera Pose and Feature Correspondence. In Proceedings of the International Conference on Computer Vision (ICCV), Venice, Italy, October 2017. Oral presentation, Marr Prize (honourable mention) [pdf] [video]
D Campbell, L Petersson, L Kneip, and H Li. Globally-optimal inlier set maximisation for camera pose and correspondence estimation. IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI), 42:328–342, 2020 [pdf (arxiv)]
D Campbell, L Petersson, L Kneip, H Li, and S Gould. The alignment of the spheres: Globally-optimal spherical mixture alignment for camera pose estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, USA, June 2019 [pdf]
L. Gao, J. Su, J. Cui, X. Zeng, X. Peng, and L. Kneip. Efficient globally-optimal correspondence-less visual odometry for planar ground vehicles. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Paris, France, May 2020 [pdf] [youtube] [bilibili]
Certifiably globally optimal solutions to non-minimal relative registration problems
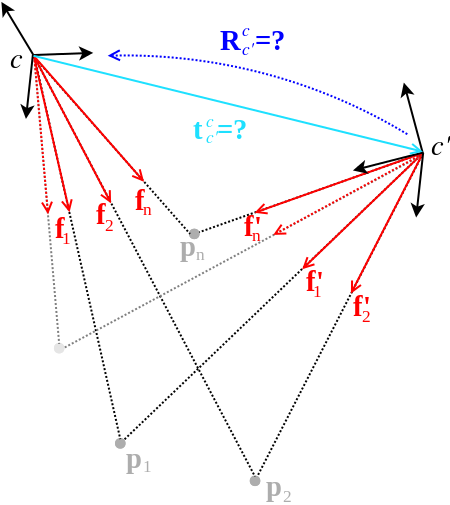
Finding the relative pose between two calibrated views ranks among the most fundamental geometric vision problems. It therefore appears as somewhat a surprise that a globally optimal solver that minimizes a properly defined energy over non-minimal correspondence sets and in the original space of relative transformations (up-to-scale SE3 transformation) was not discovered until only very recently. In one of Prof Kneip's recent collaborations, the problem is solved as a Quadratically Constrained Quadratic Program (QCQP), which can be converted into a Semidefinite Program (SDP) using Shor’s convex relaxation. Through exhaustive validation, the approach is proven to always find a certified (a-posteriori) global optimum of the cost function. In another recent work, the approach is extended to the generalized camera relative pose problem.
J Briales, L Kneip, and J Gonzalez-Jimenez. A Certifiably Globally Optimal Solution to the Non-Minimal Relative Pose Problem. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, June 2018. Oral presentation [pdf]
J. Zhao, W. Xu, and L. Kneip. A certifiably globally optimal solution to generalized essential matrix estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, USA, June 2020 [pdf] [youtube] [bilibili]
Globally optimal point set registration for minimal overlap scans of symmetric objects
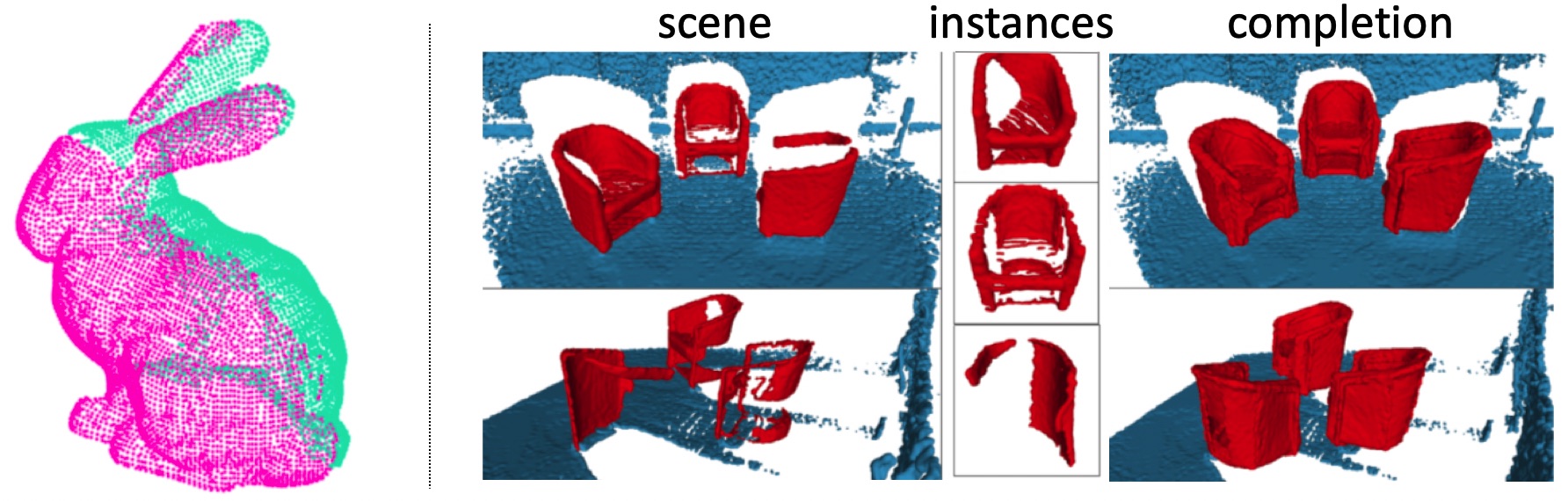
In another work we propose a solution to the challenging problem of registering two partial point sets of the same object with very limited overlap. We leverage the fact that most objects found in man-made environments contain a plane of symmetry. By reflecting the points of each set with respect to the plane of symmetry, we can largely increase the overlap between the sets and therefore boost the registration process. However, prior knowledge about the plane of symmetry is generally unavailable or at least very hard to find, especially with limited partial views. Finding this plane could strongly benefit from a prior alignment of the partial point sets. We solve this chicken-and-egg problem by jointly optimizing the relative pose and symmetry plane parameters. We present a globally optimal solver by employing the branch-and-bound (BnB) paradigm, and thereby demonstrate that joint symmetry plane fitting leads to a great improvement over the current state-of-the-art in globally optimal point set registration for common objects. As demonstrated in the figure, the method can be used to align minimal overlap scans of even just approximately symmetric objects. It can furthermore be used to perform scene completion if the same object is present multiple times in the same scan.
L. Hu and L. Kneip. Globally optimal point set registration by joint symmetry plane fitting. Journal of Mathematical Imaging and Vision (JMIV), February 2021. Open-access [pdf]
Globally optimal motion estimation for event cameras
Event cameras are bio-inspired sensors that perform well in challenging illumination conditions and have high temporal resolution. However, their concept is fundamentally different from traditional frame-based cameras. The pixels of an event camera operate independently and asynchronously. They measure changes of the logarithmic brightness and return them in the highly discretised form of time-stamped events indicating a relative change by a certain quantity since the last event. New models and algorithms are needed to process this kind of measurements. The present works look at several motion estimation problems with event cameras. The flow of the events is modelled by a general homographic warping in a space-time volume, and the objective is formulated as a maximisation of contrast within the image of warped events. Our core contribution consists of deriving globally optimal solutions to these generally non-convex problems, which removes the dependency on a good initial guess plaguing prior local optimization methods. The methods rely on branch-and-bound optimisation and employ novel and efficient, recursive upper and lower bounds derived for six different contrast estimation functions. For more information on our work on event cameras, please visit our page on geometric methods for event cameras.
X. Peng, Y. Wang, L. Gao, and L. Kneip. Globally-optimal event camera motion estimation. In Proceedings of the European Conference on Computer Vision (ECCV), Glasgow, UK, August 2020 [pdf] [youtube] [bilibili]
X. Peng, L. Gao, Y. Wang, and L. Kneip. Globally-Optimal Contrast Maximisation for Event Cameras. IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI), 2021
Accelerating Globally Optimal Consensus Maximization
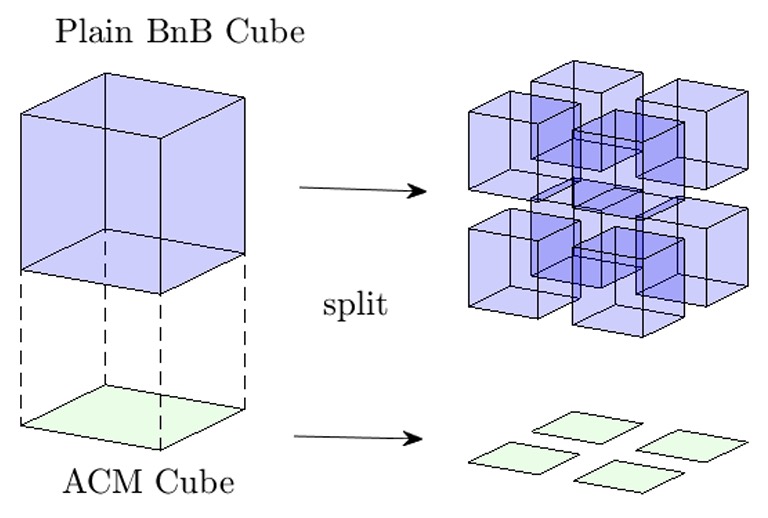
Branch-and-bound-based consensus maximization stands out due to its important ability of retrieving the globally optimal solution to outlier-affected geometric problems. However, while the discovery of such solutions caries high scientific value, its application in practical scenarios is often prohibited by its computational complexity growing exponentially as a function of the dimensionality of the problem at hand. In this work, we convey a novel, general technique that allows us to branch over an n − 1 dimensional space for an n-dimensional problem. The remaining degree of freedom can be solved globally optimally within each bound calculation by applying the efficient interval stabbing technique. While each individual bound derivation is harder to compute owing to the additional need for solving a sorting problem, the reduced number of intervals and tighter bounds in practice lead to a significant reduction in the overall number of required iterations..
X Zhang, L Peng, W Xu, and L Kneip. Accelerating Globally Optimal Consensus Maximization in Geometric Vision. IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI), 46: 4280–4297, 2024 [pdf]
Globally optimal camera resectioning under a geometric error criterion
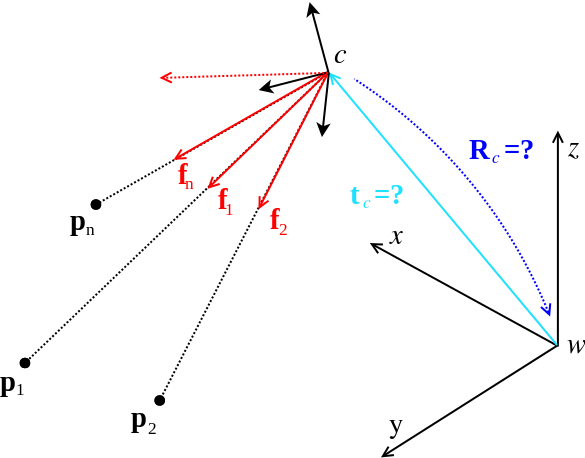
Perhaps surprisingly, the final method that appears here for globally optimal estimation is the Gröbner basis method. The targetted problem is non-minimal camera resectioning. As for other problems, there exist linear solutions that employ an algebraic error criterion (e.g. EPnP). By using the object space error formulation (point-to-ray distances), we can come up with an alternative, geometrically relevant energy minimization problem that appears in polynomial form. As it turns out, camera resectioning is simple enough so it remains possible to solve the polynomial problem resulting from the derivation of the first-order optimality conditions in closed form. The result–UPnP–is an algorithm that identifies the global minimum of a non-linear, geometrically relevant energy in closed-form! Note that in a follow-up submission, we have improved our UPnP solver by adding a classifier trained to predict the best permutation to be used inside the permutation-invariant solver. For more information on our work on camera pose estimation problems including the mentioned permutation classifier for permutation invariant solvers, please visit our page on geometric computer vision.
L Kneip, H Li, and Y Seo. UPnP: An optimal O(n) solution to the absolute pose problem with universal applicability. In Proceedings of the European Conference on Computer Vision (ECCV), Zurich, Switzerland, September 2014
W Xu, H Lan, M C Tsakiris, and L Kneip. Online stability improvement of Gröbner basis solvers using deep learning. In Proceedings of the International Conference on 3D Vision (3DV), Quebec City, Canada, September 2019. Oral Presentation




