Geometric camera pose calculation
A significant part of MPL's research agenda has since ever been devoted to the solution of fundamental geometric camera pose estimation problems. Our work covers both absolute and relative camera pose estimation problems, dealing with various aspects such as geometric optimality, degeneracies, and computational complexity in both the minimal and the non-minimal case. The below is a summary of the problems that we have worked on. Please note that many of the algorithms have been made publically available through the open-source library OpenGV, which enjoys wide popularity across both industry and academia, and can be downloaded from github:
Link: https://github.com/laurentkneip/opengv
Documentation: http://laurentkneip.github.io/opengv
Paper: L Kneip and P Furgale. OpenGV: A Unified and Generalized Approach to Calibrated Geometric Vision. In Proceedings of The IEEE International Conference on Robotics and Automation (ICRA), 2014.
[pdf]
Some of the problems require the solution of algebraic geometry formulations. We master the technique of automatic solver generation, and use our own solver generator. It is called polyjam, and also made available as an open-source package on github:
Link: https://github.com/laurentkneip/polyjam
Documentation: https://github.com/laurentkneip/polyjam/blob/master/polyjam_documentation/documentation.pdf
Please visit the Software page for more details.
Minimal Absolute Pose
Prof. Kneip's most cited work solves the Perspective-Three-Point (P3P) problem (also known as camera resectioning), which aims at determining the position and orientation of a camera in the world reference frame from three 2D-3D point correspondences. First solutions to this problem date back to at least 1841. Most solutions attempt to first solve for the position of the points in the camera reference frame, and then compute the point-aligning transformation between the camera and the world frame. The novel closed-form solver proposed by Prof. Kneip and former collaborators computes the aligning transformation directly in a single stage, without the intermediate derivation of the points in the camera frame. The resulting superior computational efficiency is particularly suitable for any RANSAC outlier-rejection step, which is always recommended before applying PnP or non-linear optimization of the final solution.
The algorithm has become a cornerstone of pose estimation in industry, and has been used at least somewhere along the way by giants like Google, Apple, Meta, and Qualcomm.
L Kneip, D Scaramuzza, and R Siegwart. A Novel Parametrization of the Perspective-Three-Point Problem for a Direct Computation of Absolute Camera Position and Orientation. In Proceedings of The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2011. (acc. rate: 22.5% posters). [pdf] [code]
n-point absolute pose with generalized cameras
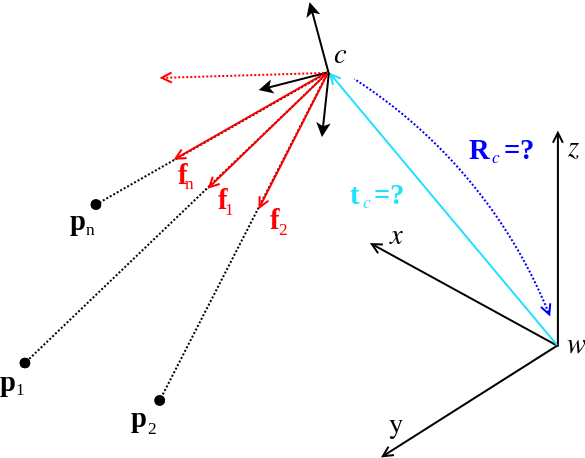
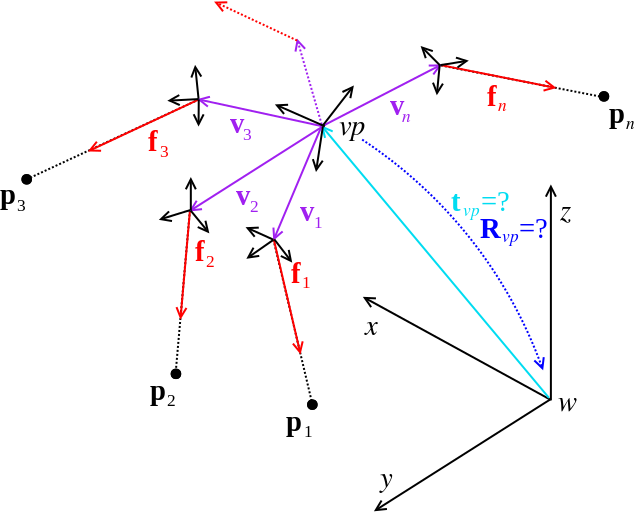
MPL has also investigated the absolute pose problem with n point correspondences, and notably in the context of generalized cameras. A generalized camera is an abstraction that allows the treatment of measurements that correspond to spatial rays that do no longer necessarily intersect in a single point. It is thus potentially different from a classical monocular camera. A practically relevant example is given by an extrinsically calibrated multi-camera system. Such a system is also called a Multi-Perspective Camera (MPC), and in its most general form the cameras do not even share overlap in their fields of view, but are pointing into arbitrary directions (Please also check out our research pages on different camera architectures, as well as 360-degree MPCs, which are commonly found in automotive applications). We developed a set of algorithms for which the complexity is linear in the number of point correspondences. Our most recent contribution, UPnP, is furthermore applicable to both central and non-central (generalized) cameras, and it computes the solution under a geometrically optimal error criterion.
L Kneip, P Furgale, and R Siegwart. Using Multi-Camera Systems in Robotics: Efficient Solutions to the NPnP Problem. In Proceedings of The IEEE International Conference on Robotics and Automation (ICRA), Karlsruhe, 2013 (best computer-vision paper award finalist). [pdf]
L Kneip, H Li, and Y Seo. UPnP: An Optimal O(n) Solution to the Absolute Pose Problem with Universal Applicability. In Proceedings of The European Conference on Computer Vision (ECCV), 2014.
Minimal and non-minimal rotation-only relative pose solvers for central and non-central camera systems
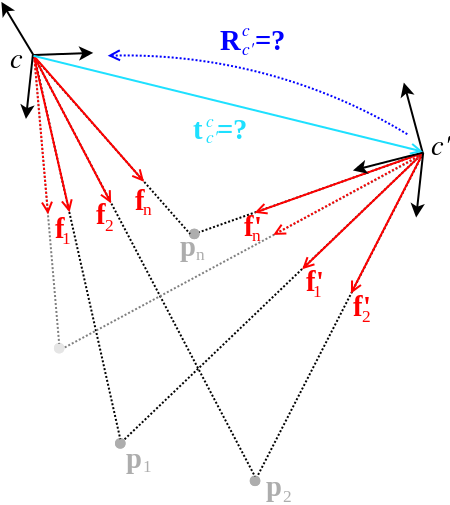

We also looked into the relative pose problem, and notably developped solutions that solve for the rotation independently of the translation. Besides a minimal solution for the central case, we also developped a suite of non-minimal iterative solvers for central and non-central camera systems. Especially in the non-central case, embedding the algorithm into a robust sampling scheme provides a very good trade-off between the number of employed point correspondences and computational efficiency. Note again that a very common non-central camera system used in the context of smart vehicles is given by a 360-degree surround-view multi-perspective camera. Our WACV'16 contribution–the final step in this series–provides the first fully general solution to the generalized relative pose and scale problem, a problem in which two generalized cameras are registered with respect to each other, knowing that they are calibrated only up to an unknown relative scale factor. Treating scale-invariant view-graphs as virtual generalized cameras, this algorithm enables us to determine the similarity transformation between pairs of view-graphs directly from the original 2D-2D point correspondences (and thus avoids the use of noisy triangulated points). Important applications are given by loop closure in visual SLAM and hierarchical structure from motion.
L Kneip, R Siegwart, and M Pollefeys. Finding the Exact Rotation Between Two Images Independently of the Translation. In Proceedings of The European Conference on Computer Vision (ECCV), 2012. [pdf]
L Kneip and S Lynen. Direct Optimization of Frame-to-Frame Rotation. In Proceedings of The International Conference on Computer Vision (ICCV), 2013. [pdf]
L Kneip and H Li. Efficient computation of Relative Pose for Multi-Camera Systems. In Proceedings of The IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 2014. [pdf]
L Kneip, C Sweeney, and R Hartley. The generalized relative pose and scale problem: View-graph fusion via 2D-2D registration. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision (WACV), 2016.
C Sweeney, L Kneip, T Höllerer, and M Turk. Computing Similarity Transformations from Only Image Correspondences. In Proceedings of The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2015. [pdf]
Special configurations
In addition to the above mentioned cases, we have also spent a significant amount of time on the development of geometric pose calculation methods for the following special configurations:
Single camera plus IMU:
L Kneip, M Chli, and R Siegwart. Robust real-time visual odometry with a single camera and an IMU. In Proceedings of the British Machine Vision Conference (BMVC), Dundee, Scotland, August 2011. Oral presentation [pdf] [youtube]
In this work we solve the central absolute and relative pose estimation problems for the special case where relative rotations with respect to a prior time are already known. The proposed solvers only use at most 2 correspondences. The solvers have been proposed as part of an efficient visual-inertial estimation framework. Please visit our page on visual SLAM solutions for more information.
Relative pose in piece-wise planar environments:
Y Zhou, L Kneip, and H Li. A revisit of methods for determining the fundamental matrix with planes. In Proceedings of the Digital Image Computing on Techniques and Applications (DICTA), Adelaide, Australia, November 2015. [pdf]
Relative pose calculation from ray-point-ray features:
J Zhao, L Kneip, Y He, and J Ma. Minimal case relative pose computation using ray-point-ray features. IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI), 2020.
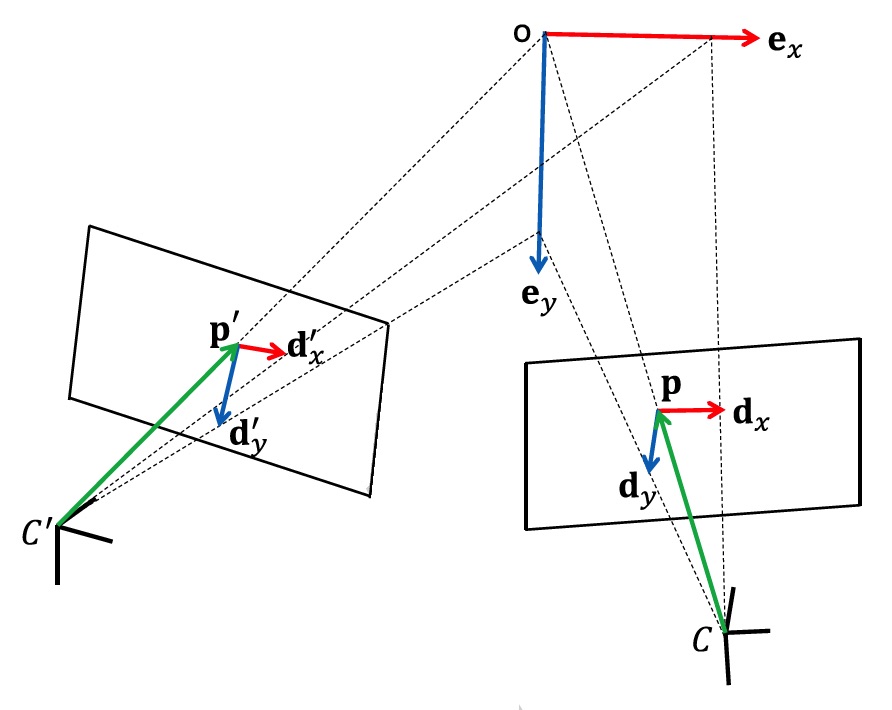
In this work we explore augmented image corner information. In particular, we make the assumption that an image corner is made up of two intersecting straight lines, and that the direction of the reprojection of those lines can be measured in the image and used as an additional constraint on the relative pose estimation problem.
Relative pose estimation for non-holonomic vehicles:
K Huang, Y Wang, and L Kneip. Motion estimation of non-holonomic ground vehicles from a single feature correspondence measured over n views. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2019. [pdf] [youtube] [bilibili]

Geometric relative pose solver that uses the constrained motion model of the Ackermann vehicle on which the sensor is mounted. More related methods can be found on the vision for Ackermann vehicles page.
- We developed many more geometric methods in the context of calibration, globally optimal (including correspondence-free) methods, point set registration, etc. Please keep exploring.
Learning online selection strategies for polynomial solver generation
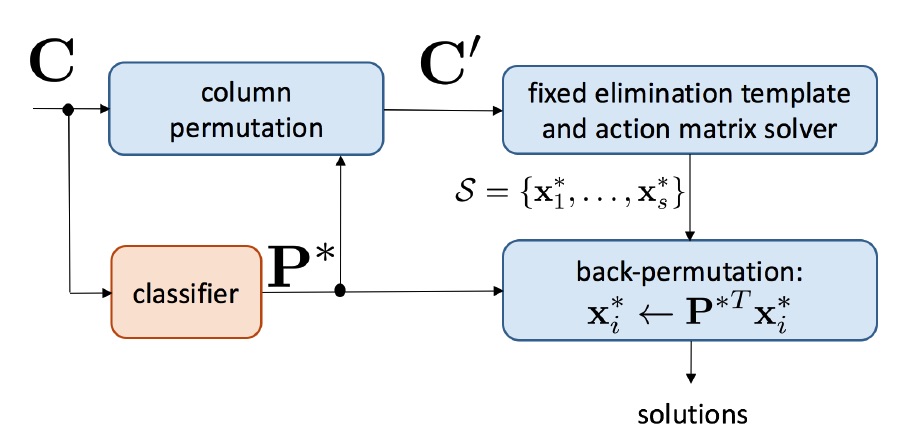
Over the past decade, the Gröbner basis theory and automatic solver generation have lead to a large number of solutions to geometric vision problems, some of which are part of the above listing. In practically all cases, the derived solvers apply a fixed elimination template to calculate the Gröbner basis and thereby identify the zero-dimensional variety of the original polynomial constraints. However, it is clear that different variable or monomial orderings lead to different elimination templates, and our research has shown that they may present a large variability in accuracy for a certain instance of a problem. The below work shows two contributions:
- It shows that for a common class of problems in geometric vision, variable reordering simply translates into a permutation of the columns of the initial coefficient matrix, and that—as a result—one and the same elimination template can be reused in different ways, each one leading to potentially different accuracy.
- It then proves that the original set of coefficients may contain sufficient information to train a classifier for online selection of a good solver, most notably at the cost of only a small computational overhead. The method has wide applicability which is demonstrated at the hand of generic dense polynomial problem solvers, as well as a concrete solver from geometric vision.
W Xu, H Lan, M C Tsakiris, and L Kneip. Online stability improvement of Gröbner basis solvers using deep learning. In Proceedings of the International Conference on 3D Vision (3DV), Quebec City, Canada, September 2019. Oral Presentation
Spatio-temporal geometric solvers for event camera motion calculation
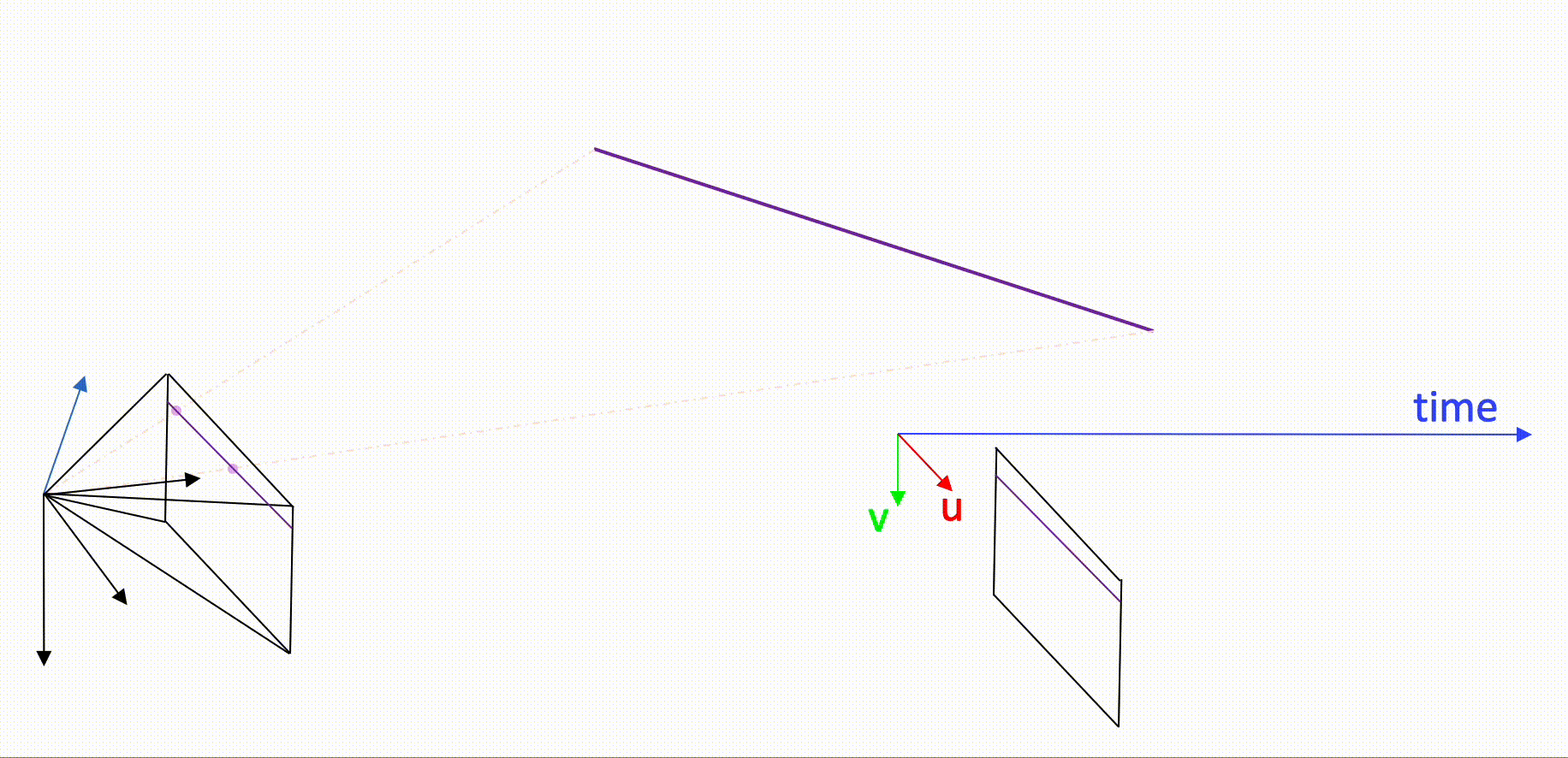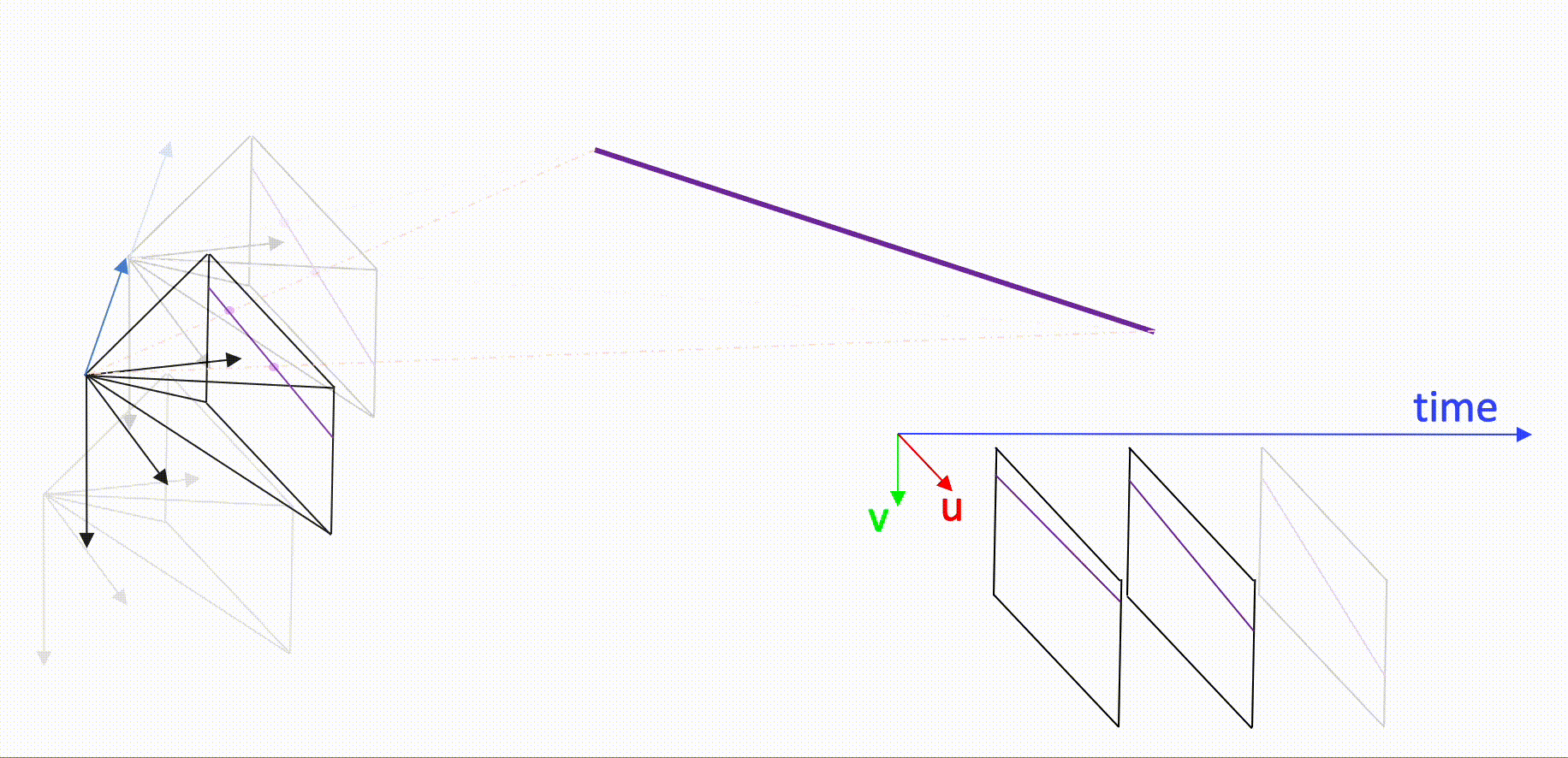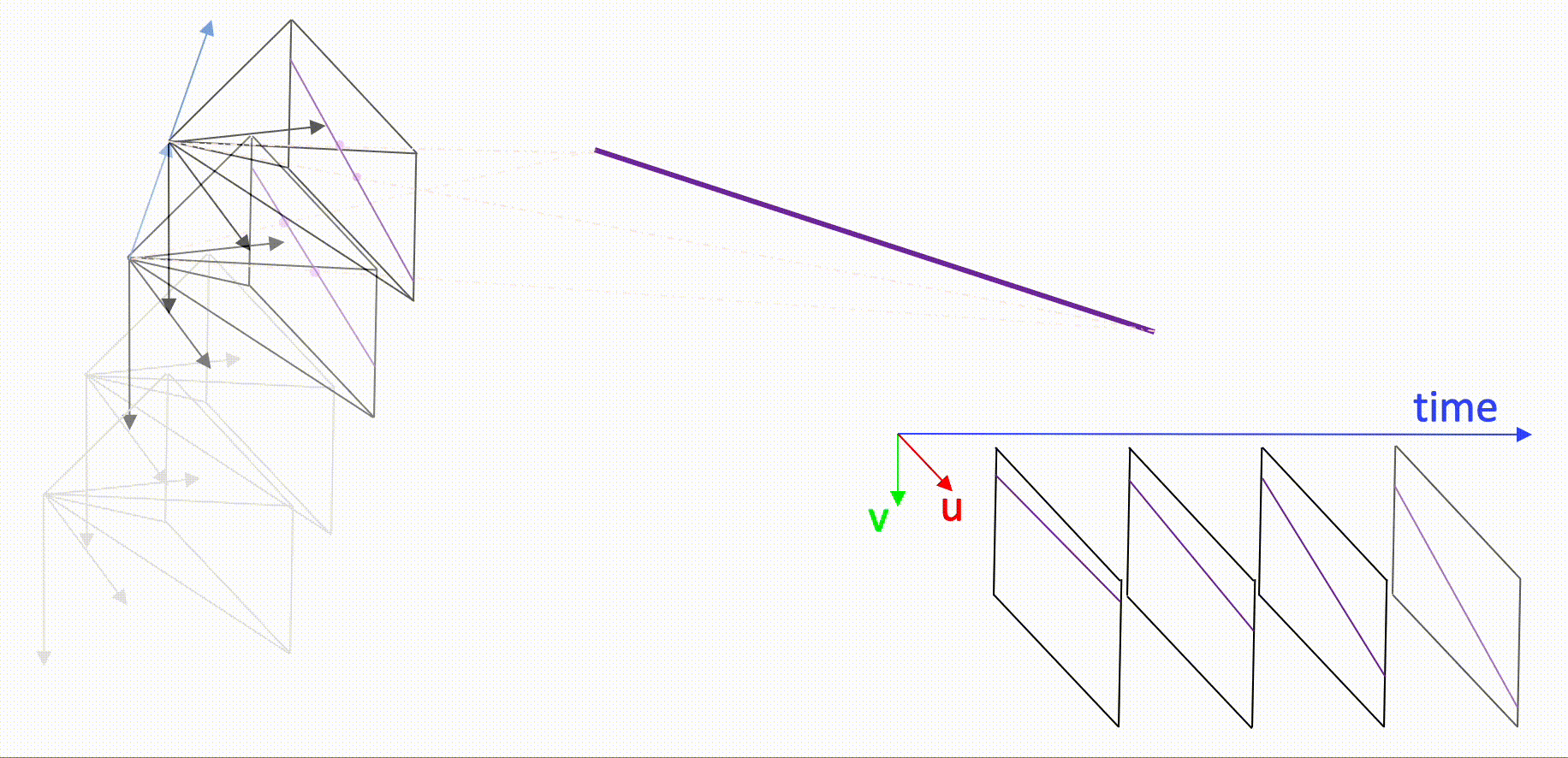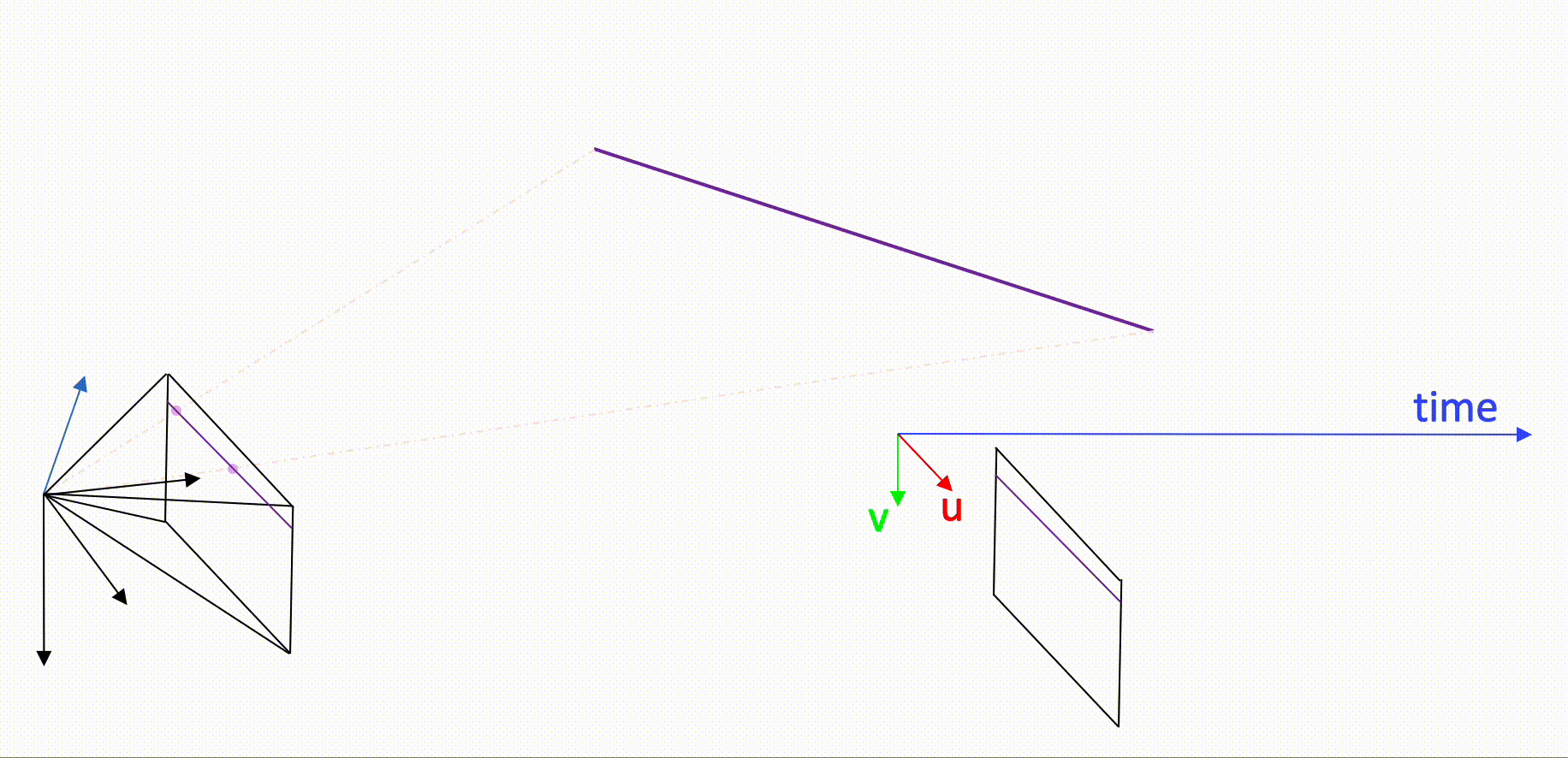
Calculating the relative displacement of an event camera is a challenging topic as it is difficult to pursue classical solution strategies that rely on feature extraction and matching followed by robust geometric fitting (e.g. Ransac). The reason is that events simply do not form quasi-instantaneous frames in which one could easily detect corners or lines. There are certainly methods that bypass via the creation of frame-like representations (such as frames of accumulated events, time surface maps, etc.), but these methods tend to ignore temporal information somewhere along the process and are therefore inexact. At MPL, we have initiated a new line of research in which we try to characterize exact geometric models that explain the location in space and time of single events under certain conditions. For example, if a camera observes a straight line under locally constant linear displacement, the location of the events generated by this line can be described by an exact parametric model that depends on the relative line geometry as well as partial velocity parameters. It is a beautiful theory that not only enables exact motion estimation through a single, parametric event clustering technique, but also a general handling of spatio-temporally sampling sensors. Check out our event camera page to learn more about this exciting technology and our geometric solution approach.
X. Peng, W. Xu, J. Yang, and L. Kneip. Continuous Event-Line Constraint for Closed-Form Velocity Initialization. In Proceedings of the British Machine Vision Conference (BMVC), 2021. [pdf]
L. Gao, H. Su, D. Gehrig, M. Cannici, D. Scaramuzza, and L. Kneip. A 5-Point Minimal Solver for Event Camera Relative Motion Estimation. In Proceedings of the International Conference on Computer Vision (ICCV), 2023. Oral Presentation. [pdf] [video] [code]
L. Gao, D. Gehrig, H. Su, D. Scaramuzza, and L. Kneip. An n-point linear solver for line and motion estimation with event cameras. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2024. Oral presentation (0.8% acceptance rate!). [pdf] [code] [video]
W. Xu, S. Zhang, L. Cui, X. Peng, and L. Kneip. Event-based visual odometry on non-holonomic ground vehicles. In Proceedings of the International Conference on 3D Vision (3DV), 2024. [pdf] [code] [video]
W. Xu, X. Peng, and L. Kneip. Tight Fusion of Events and Inertial Measurements for Direct Velocity Estimation. IEEE Transactions on Robotics (T-RO), 40:240–256, 2023. [pdf]
Z. Ren, B. Liao, D. Kong, J. Li, P. Liu, L. Kneip, G. Gallego, and Y. Zhou. Motion and structure from event-based normal flow. In Proceedings of the European Conference on Computer Vision (ECCV), 2024. [pdf]




